Алгоритм методу
Головною перевагою методу є можливість розбиття на скінченні елементи області будь-якої форми і, таким чином, можливість розрахунку полів напружень і деформацій в реальних деталях з урахуванням всіх їх конструктивних особливостей.
Розбиття на скінченні елементи. Розмір елементів можна змінювати, зменшуючи його поблизу цікавить області, і збільшуючи - для зниження витрат процесорного часу
Розв'язок методом скінченних елементів двомірної магнитностатичної завдачі (лінії і колір означають напрям і величину магнітної індукції)
Точний розв'язок задачі, з нульовими значеннями на кінцях (блакитна лінія), і апроксимація цієї функції відрізками (червона).
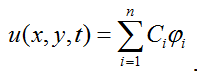Базисні функції (блакитні лінії) і лінійна комбінація з них, яка апроксимує шукану функцію (червона).
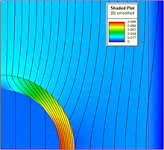
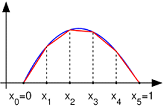
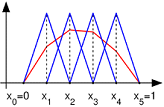
Головною проблемою чисельного рішення диференціальних рівнянь є вибір апроксимації функцій. МСЕ пропонує вибирати так звані базисні функції-форми, після чого передбачуване рішення буде лінійною комбінацією даних функцій.
У даному випадку будуть використовуватися лінійні функції-форми.
Апроксимація шуканих функцій буде проводитися за допомогою зважених нев'язок.
В першу чергу вводиться нев'язка апроксимації:
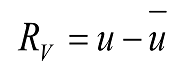(1)
Де u - точне рішення параболічного рівняння, ū - наближене рішення. Щоб зменшити дану невязку, вимагатимемо рівності нулю інтеграла по області V від похибки R помноженої на вагові функції:
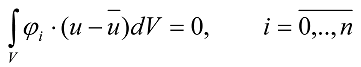(2)
Зауважимо, що в загальному випадку рівняння має вигляд:
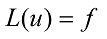(3)
Якщо крайові умови представити у вигляді:
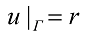(4)
Де Г-границя області. Тоді до нев'язки рівняння додається невязка на границі:
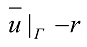(5)
Тепер, аналогічно (2) мінімізуємо суму нев'язок на границі і в області:
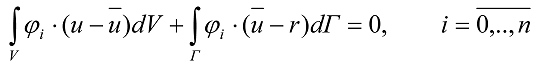(6)
Підставляючи загальний вигляд розв'язку в (6) маємо систему лінійних алгебраїчних рівнянь відносно Сi, i=1..n.
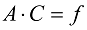
Після рішення даної системи ми можемо обчислити значення шуканої функції в будь-якій точці області V.
Для вирішення даної системи необхідно також вибрати конкретний вид функцій форми
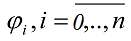
Також, варто зауважити, що ми намагаємося апроксимувати диференціальне рівняння другого порядку лінійними скінченними елементами. Водночас, порядок скінченних елементів не може бути менше порядку старшої похідної рівняння (6). Однак, можна послабити цю вимогу, перевівши рівняння в слабку (варіаційну) форму. Продемонструємо це на довільному інтегралі по скінченному елементу Vi, який розглянемо тільки біля другої похідної:
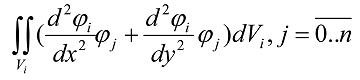
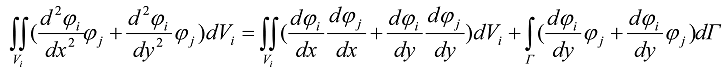(7)
Другий доданок (7) завжди рівен нулю, бо базисні функції на границі завжди обертаюсться в нуль.
Зауважимо також, що в випадку нестаціонарного рівняння та початкових умов розв'язок рівняння шукається в наступному виді:
(8)
Із тих же міркувань що і раніше, отримуємо систему диференціальних рівнянь:
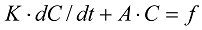(9)
Ця система розв'язується за допомогою різницевої схеми Кранка-Ніколсона.
, де φi базисні функції, а Ci - коефіцієнти, апроксимуючі шукану функцію базисними.
